Data Structure(9) - Binary Search Tree

What is Binary Search Tree?

---

Binary Search Tree allows to maintain a sorted list of numbers. It is because Binary Search Tree is also a kind of Binary Tree, it has 2 children nodes. But there is a rule for Binary Search Tree. The left node of the parent node must be smaller than parent node and the right node of the parent node must be bigger than parent node.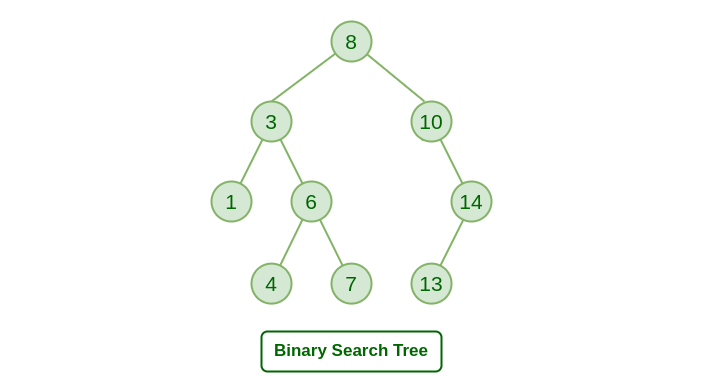

The thing we need to be careful is Binary Search Tree’s children nodes cannot be bigger or smaller than root’s value. Let me show you an example. 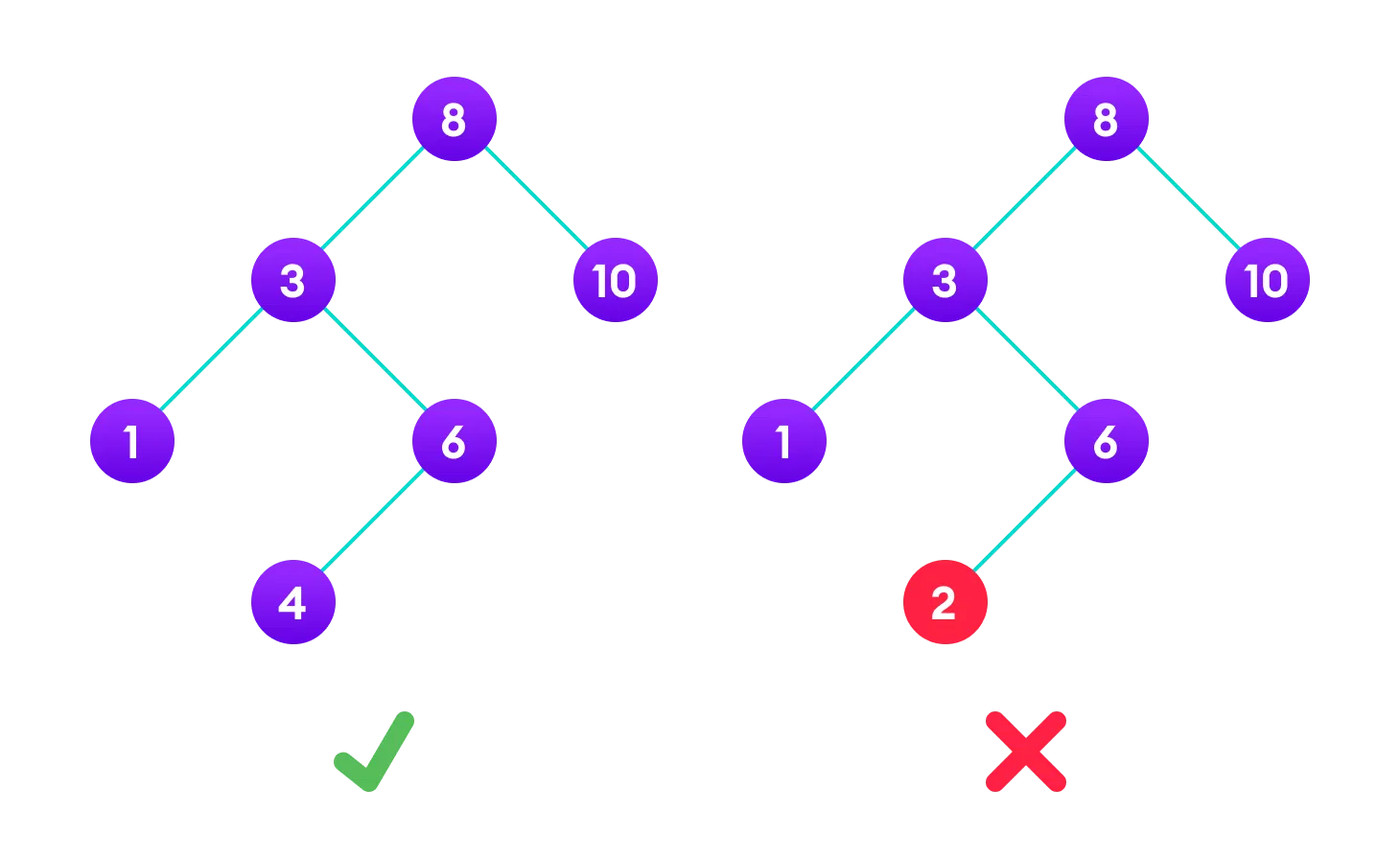In this case, 2 cannot be in there because it is smaller than 3. So, once a child node goes to right, the following all nodes need to be bigger than the value of root. 6 is bigger than 3. The list of numbers which can be the left node of 6 is { 4, 5 }. And the list of numbers which can be the right node of 6 is { 7 } because it needs to be smaller than 8.

C# doesn’t support a class for binary search tree. So, we are going to use same class as last time we used for tree and binary tree.

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

Example Problem

---

Let’s solve Validate Binary Search Tree!

Problem Description:
Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.

Example 1:

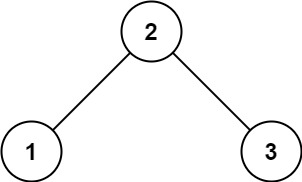
Input: root = [2,1,3]
Output: true

Example 2:

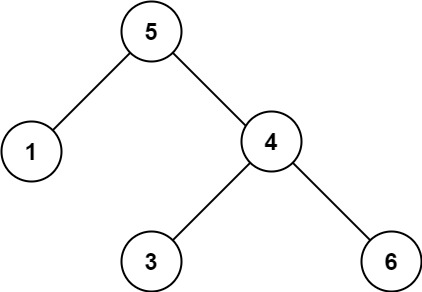
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node’s value is 5 but its right child’s value is 4.

Constraints:
The number of nodes in the tree is in the range [1, 104].
-2^31 <= Node.val <= 2^31 - 1

public class Solution {
    public bool IsValidBST(TreeNode root) {
        // In constraints, the range of Node.val is same with integer range.
        // To cover all integer range, I chose Int64(long) not Int32.
        return valid(root, Int64.MinValue, Int64.MaxValue);
    }

    // This method is to check if the node value is in between min number and max number
    public bool valid(TreeNode node, long min, long max) {
        if(node == null) {
            return true;
        }
        if (!(node.val > min && node.val < max)) return false;

        // if we want to check the left node,
        // min should be same but the max number needs to be changed to node value.
        // or if we want to check the right node,
        // max should be same but the min number needs to be changed to node value.
        return valid(node.left, min, node.val) && valid(node.right, node.val, max);
    }
}