Data Structure(8) - Tree

What is Tree?

---

Tree is a nonlinear hierachical data structure. If you imagine a tree, there is a root of tree and so many branches from root. Tree data structure is a reversed version of real tree. 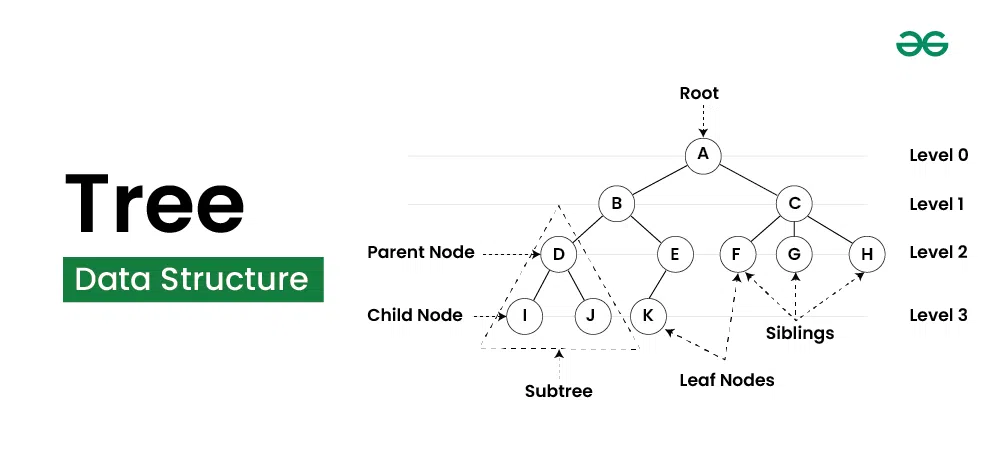Every root can have branches and every branch can be another root.

What is Binary Tree

---

Binary Tree is similar with tree structure but the only one difference is that one root can have only 2 branches.

Tree in C#

---

Unfortunately, there is no class for tree or binary tree in C#.
So, Let’s create a simple binary tree node!

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

As you can see val is a root of the tree and each val has left tree and right tree.
To understand tree structure we are going to solve 2 problems!

Example Problem

---

Problem 1

Let’s solve Same Tree!

Problem Description:
Given the roots of two binary trees p and q, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

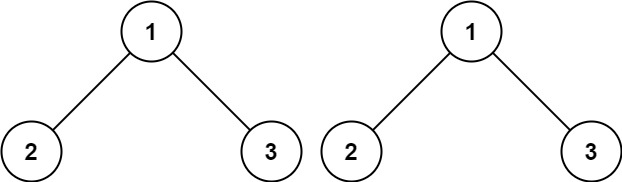
Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:

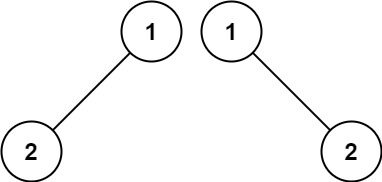
Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:

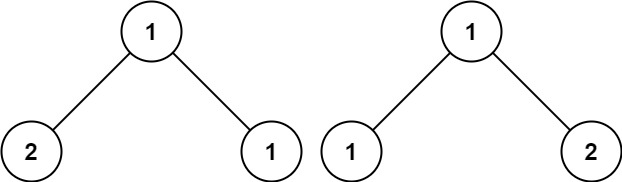
Input: p = [1,2,1], q = [1,1,2]
Output: false

public class Solution {
    public bool IsSameTree(TreeNode p, TreeNode q) {
        // if params p and q are null return true;
        if (p == null && q == null) {
            return true;
        }

        // if just one tree node is null or the root values are diffener return false;
        if (p == null || q == null || p.val != q.val) {
            return false;
        }

        // call this method again(recursive) to check each tree's left side and right side
        return IsSameTree(p.left, q.left) && IsSameTree(p.right, q.right);
    }
}

Problem 2

Let’s solve Symmetric Tree!

Problem Description:
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

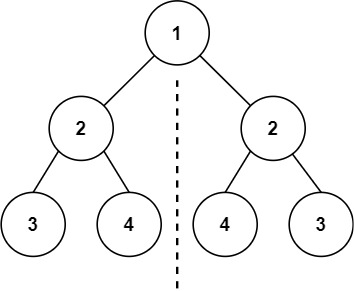
Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

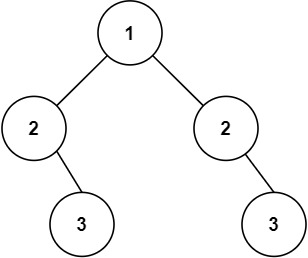
Input: root = [1,2,2,null,3,null,3]
Output: false

public class Solution {
    public bool IsSymmetric(TreeNode root) {
        // if the root node is null, just return true
        if (root == null) {
            return true;
        }

        // if not, we are going to compare left node and right node using IsMirror() method
        return IsMirror(root.left, root.right);
    }

    // To compare the left node and right node
    public bool IsMirror(TreeNode left, TreeNode right) {
        // if the left and right node are null, return true
        if (left == null && right == null) {
            return true;
        }

        // if just one of the node is null, return false
        if (left == null || right == null) {
            return false;
        }

        // We have to check 3 things
        // 1. the left's value and right's value are same
        // 2. left's left value and right's right value are same
        // 3. left's right value and right's left value are same
        return left.val == right.val && IsMirror(left.left, right.right) && IsMirror(left.right, right.left);
    }
}