Data Structure(10) - Graph

What is Graph?

---

Graph is consisted of nodes and edges. Unlike Tree structure is a directed graph, Graph is undirected graph.

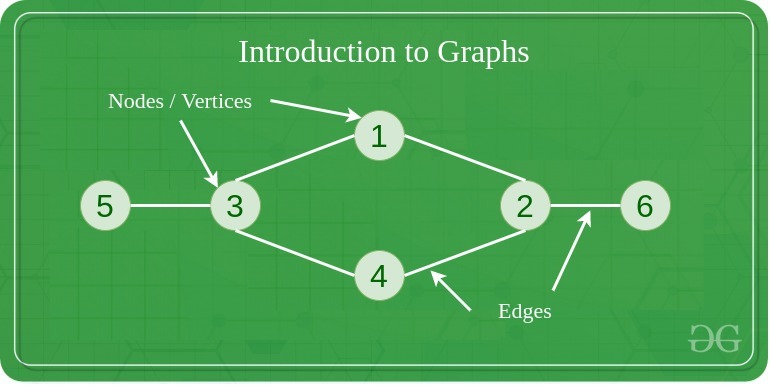
In this picture, there are 6 nodes and 6 edges.

• Node: 1, 2, 3, 4, 5, 6
• Edge: [1, 2], [1, 3], [3, 4], [2, 4], [2, 6], [3, 5]

Adjacency Matrix

We can respreesnt a graph in adjacency matrix.

	1	2	3	4	5	6
1	0	1	1	0	0	0
2	1	0	0	1	0	1
3	1	0	0	1	1	0
4	0	1	1	0	0	0
5	0	0	1	0	0	0
6	0	1	0	0	0	0

All of nodes can be connected other nodes without direct and rules.

There is no specific class for graph in C#. So, We can use below class.

public class Node {
    public int val;
    public IList<Node> neighbors;

    public Node() {
        val = 0;
        neighbors = new List<Node>();
    }

    public Node(int _val) {
        val = _val;
        neighbors = new List<Node>();
    }

    public Node(int _val, List<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}

As you can see in the code, each node has value, and neighbors defined as list of node. Using this class, we can create a node and add a new neighbor for the node.

How can we find a node?
If all nodes are connected, it means we can find a node using another node. But there would be so many way to reach the node. For example, the picture in the above, if the starting point is 5 and destination point is 6, then there is be 2 ways to reach 6.

1. 5 -> 3 -> 1 -> 2 -> 6
2. 5 -> 3 -> 4 -> 2 -> 6

So, everytime we search a node, we need to think what is the most efficient way to find it. There is 2 ways to search a node. To understand these ways, I brought a question and solved 2 different ways.

Example Problem

---

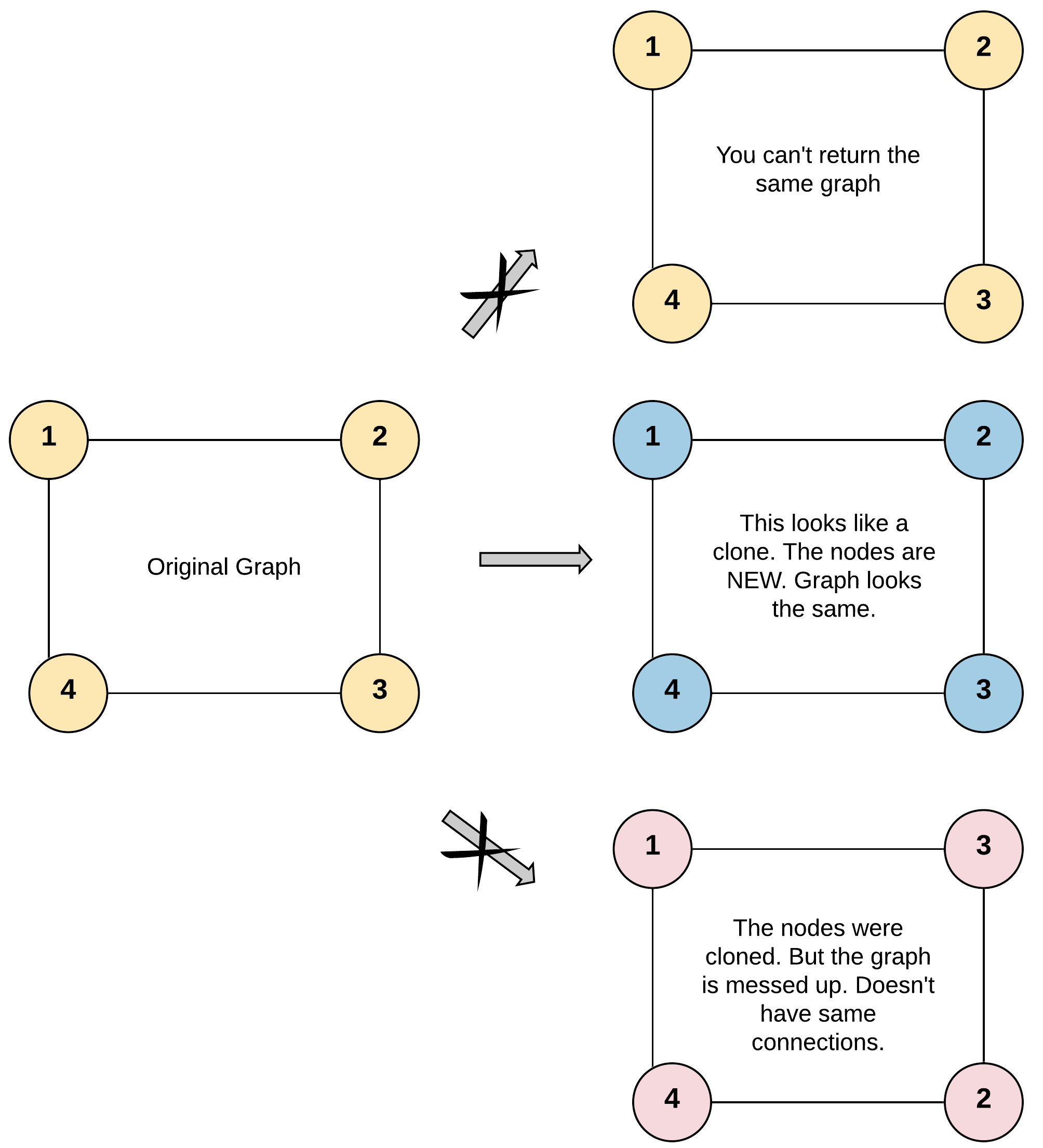
Let’s solve Clone Graph!

Problem Description:
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:
For simplicity, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)’s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)’s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)’s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)’s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

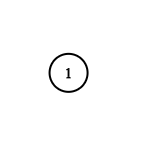
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:
Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Depth First Search(DFS)

---

Depth First Search is used when the node we want to find is in very below from the starting point. DFS Algorithm is using Stack and the flow is followed as below.

1. Put the starting point node into Stack.
2. Take one node from Stack and put every neighbors into stack. (needs to be marked as visited)
3. If the neighbor is already marked as visited, don’t put the node into stack.
4. Repeat 2 and 3 until all node marked as visited

public class Solution {
    /// Difined a dictionary to check if all the node are visited
    Dictionary<int, Node> visited = new Dictionary<int, Node>();

    public Node CloneGraph(Node node) {
        // if the node is empty just return null
        if(node == null) {
            return null;
        }

        // copy the input node
        Node src = new Node(node.val);
        // save the node with 
        visited.Add(src.val, src);

        // copy all the neighbors of the src node
        foreach(Node neighbor in node.neighbors) {
            // if the neighbor has not been visited
            if(!visited.ContainsKey(neighbor.val)) {
                // by calling current method recursive,
                // we can copy the neighbor node
                Node cloneNeighbor = CloneGraph(neighbor);
                src.neighbors.Add(cloneNeighbor);
            // the neighbor already visited.
            } else {
                // add the neighbor node from visited node to src's neighbor
                src.neighbors.Add(visited[neighbor.val]);
            }
        }

        return src;
    }
}

Breath First Search(BFS)

---

Breath First Search is used when the graph depth is not that deep and the width of the graph is very wide. Unlike DFS Algorithm uses Stack, BFS Algorithm uses Queue and the flow is followed as below.

1. Add the starting point node into queue.
2. Take a node from queue and add all neighbors into queue(to be marked as visited)
3. If the neighbor is already marked as visited, don’t put the node into Queue.
4. Repeat 2 and 3 until all node marked as visited

public class Solution {
    public Node CloneGraph(Node node) {
        if(node == null) {
            return null;
        }

        // Queue for visiting all node
        Queue<Node> queue = new Queue<Node>();
        // for marking all node as visited
        Dictionary<Node, Node> visited = new Dictionary<Node, Node>();

        // Clone the input node
        visited.Add(node, new Node(node.val));
        queue.Enqueue(node);

        while(queue.Count != 0) {
            // Take one from Queue
            Node current = queue.Dequeue();

            foreach(Node neighbor in current.neighbors) {
                if(!visited.ContainsKey(neighbor)) {
                    // Clone the input node's neighbors
                    visited.Add(neighbor, new Node(neighbor.val));
                    queue.Enqueue(neighbor);
                }

                // Add neighbors to node
                visited[current].neighbors.Add(visited[neighbor]);
            }
        }

        return visited[node];
    }
}